sześcian magnetyczny :) Cramp: 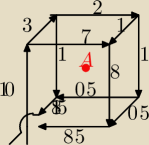mógłby ktoś pomóc? w zadaniu muszę obliczyć natężenie pola magnetycznego w punkcie A. Punkt A jest środkiem sześcianu takiego jak na rysunku, którego krawędź boczna jest równa a=1m. Natężenie i kierunek płynięcia prądów jak na rysunku.

MQ: !. wYcałkować sobie, z prawa Biota − Savarta, http://fizyka.pisz.pl/strona/228.html pole dla jednego odcinka (albo znaleźć gdzieś wzór na sieci) i potem skorzystać z superpozycji pól.

Cramp: że ten wzór? I/2πr

Cramp: sorry za moją niewiedze, ale jestem zwykłym uczniem 3 kl LO.

olimpijczyk: Na początek wyraź to pole jako B=B_i gdzie B_i to pole pochodzące od jednego przewodu. Po prostu dodaj te wektory.

daras: a czy to nie jest przypadkiem zadanie z olimpiady fizycznej?

Cramp: dostaliśmy je na lekcji jako zadanie na 5, być może że jest z olimpiady

Cramp: pole magnetyczne wytwarza się naokoło przewodnika z prądem, przewodnikiem są krawędzie sześcianu

daras: Zastosuj zasadę superpozycji, najpierw wyznacz odległosć środka sześcianu od krawędzi−czysta geometria, a następnie podstaw do wzoru na indukcję. Czy jak rozwiażę to dostane za ciebie 5 ?

Cramp: już nie chodzi o 5 bo zadanie było na dziś, ale zaciekawiło mnie jak to rozwiązać, to że mam obliczyć odległość i podstawić do wzoru na indukce to wiem, ale tu pojawia się pytanie co z plusami i minusami, bo w różny sposób mogę patrzeć na sześcian i różne wyniki otrzymuję albo czegoś nie rozumiem.

Cramp: i czasem nie do wzoru na natężenie pola? H=I/4πr ?

qwerty: mógłbym prosić o pomoc w moim temacie

daras: To w jaki sposób patrzysz na sześcian nie ma znaczenia, ustal sobie dla wygody któryś róg w początku swojego układu współrzędnych. Najważniejsze to ustalić , w którą stronę płyną prądy we wszystkich krawędziach a potem stosujesz regułę prawej ręki i dodajesz wektory.

daras:

	I
PS. H =		, gdzie d − odległość środka sześcianu od krawędzi
	2πd

tak naprawdę problem jest bardziej skomplikowany, bo krawędzie nie są nieskończenie długie i należałoby pocałkować ale na poziomie szkoły średniej stosujemy przybliżony wzór podany wyżej

daras: 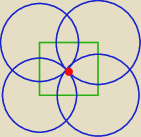w punkcie A należy rozważyć sumy wektorów natężeń pól pochodzących od 4 krawędzi w danym rzucie( czyli kierunku patrzenia), takich czwórek będzie 3 tyle ile wymiarów w przestrzeni pamiętaj, że wszystkie wektory są styczne do okręgów przechodzących przez A a ich zwrot zalezy od kierunku przepływu prądu w danej krawędzi (reguła korkociągu, śruby, prawej ręki itp.)