Proszę o pomoc z zadaniem z dynamiki z@gubiona: Ciało zsuwa się swobodnie z wierzchołka równi pochyłej. Wyznacz prędkość ciała na końcu równi i czas ruchu, jeżeli wysokość równi h=25m, a jej kąt nachylenia do poziomu α=60st. a) pomijając tarcie, b) z uwzględnieniem tarcia (współczynnik tarcia f=0,5)

daras: i jak się zamierzasz za to zadanie zabrać ?

z@gubiona: 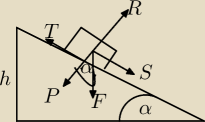Wiem, że F=mg S=ma v=at a) 1. S/F=sinα ⇒ S=Fsinα P/F=cosα ⇒ P=Fcosα 2. S=ma ⇒ a=S/m=Fsinα/m=mgsinα/m=gsinα 3. prędkość końcową wyznaczam ze wzoru v_k²=v₀²+2as v_k²=2gsinα*h/sinα, bo h/s=sinα ⇒ s=h/sinα v_k²=2gh v_k=√2gh I tym samym zrobiłam niechcący podpunkt a)

daras: tylko do oznaczania siły zsuwającej używaj innego symbolu, bo S −to zazwyczaj droga np. F_s = mg sinα a = gsinα − przyspieszenie bez tarcia Najszybszy sposób wyznaczenia predkości końcowej, polega na skorzystaniu z ZZEnergii: bez tarcia: E_k = E_p => v_k = √2gh a z uwzględnieniem tarcia : E_k = E_p + W_T, gdzie praca siły tarcia W_T = Ts i tu musisz podstawić to, co policzyłaś z trygon.