Łódź przepływa na drugi brzeg rzeki kierując się pod kątem 45 stopni. Rebel: Łódź kieruje się pod kątem 45 stopni do linii brzegu, z prądem rzeki o szerokości 240 m. Prędkość łodzi względem wody wynosi 2m/s. Prędkośc rzeki wynosi 1m/s. Łódź przepływa na drugą stronę rzeki. Policz o ile wzdłuż linii brzegu łódź przesunie się w czasie ruchu na drugi brzeg? W układzie odniesiena wody liczę, że czas ruchu łodzi wynosi około 170 sekund. Oznacza to, że łódź zostanie zniesiona przez wodę o 170 metrów. Jak policzyć o ile wzdłuż linii brzegu łódź się przesunie?

MQ: Skoro płynie pod kątem 45 stopni, to w układzie odniesienia rzeki tyle przepłynie wzdłuż, co w poprzek, bo masz trójkąt prostokątny równoramienny, więc wzdłuż brzegu przepłynie twoje wyliczone 170m plus tyle co szerokość rzeki, czyli plus 240m.

Rebel: Ale łódź nie płynie pod kątem 45 stopnii do linii brzegu tylko kieruje się pod kątem 45 stopni do linii brzegu.

Rebel: Czy przy zniesieniu rzeki ten kąt przypadkiem nie ulega zmniejszeniu? Z tego co piszesz wychodzi na to, że obrazek w układzie odniesienia rzeki i wody wyglądałby tak samo?...

MQ: Ja rozumiem to tak, że dziób ma skierowany pod kątem 45 st do brzegu, więc jej wektor prędkości w układzie rzeki ma kąt 45 st.

MQ: BTW układ odniesienia rzeki to układ odniesienia wody. Układ nieruchomy, to układ odniesienia brzegu.

Rebel: 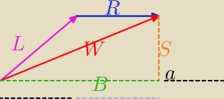L − wektor łódki w układzie odniesienia rzeki tak jak mówisz pod kątem 45st do brzegu rzeki B R − wektor prądu rzeki W − wypadkowa tych wektorów, czyli ruch łódki w układzie rzeki S − szerokość rzeki a − kąt alfa równy 45 st Oznacza to, że łódka jest skierowana pod kątem 45 st do brzegu ale nie płynie pod takim kątem, dobrze myślę? W każdym razie z rysunku już widzę dlaczego trzeba to dodać.

Rebel: Piszac układ odniesienia wody miałem na myśli układ odniesienia ziemii (lub brzegu jak kto woli).

MQ: Dobrze myślisz.

Rebel: Dzięki wielkie za pomoc!