fizyka.pisz.pl
forum zadankowe
matematyka w fizyce
kinematyka
dynamika
ruch obrotowy
pole grawitacyjne
teoria względności
siły sprężystości i drgania mechaniczne
fale mechaniczne
akustyka
elektrostatyka
prąd elektryczny
magnetyzm
indukcja i fale elektromagnetyczne
optyka
światło i atom
termodynamika
hydrostatyka
ciało stałe
przemiany jądrowe
gra w kropki
Kinematyka rzuty ukosne
aaaaaaaa:
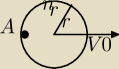 Z jaką prędkością powinno toczyć się koło po poziomej powierzchni
, aby małe ciało, które oderwało się od tego koła z punktu A,
po przebyciu pewnej drogi w
powietrzu ponownie trafiło do
tego samego punktu na kole
po wykonaniu przez koło całkowitej liczby obrotów. Promień koła wynosi R.
(zb zadań Mendel, 245)
Próbowałem porównać zasięg rzutu z n obrotami koła, ale to do niczego nie doprowadziło
Wydaje mi się, że w punkcie a Całkowita prędkość jest V0 pionowa i V0 pozioma, więc kąt rzutu
powinnen się równać 45st.
Mam wrażenie , że trzeba uzależnić ilość obrotów koła od zasięgu.
Odpowiedzi podają wynik v0 = √πRg
Poproszę o jakąś wskazówkę i z góry dziękuję za pomoc
Z jaką prędkością powinno toczyć się koło po poziomej powierzchni
, aby małe ciało, które oderwało się od tego koła z punktu A,
po przebyciu pewnej drogi w
powietrzu ponownie trafiło do
tego samego punktu na kole
po wykonaniu przez koło całkowitej liczby obrotów. Promień koła wynosi R.
(zb zadań Mendel, 245)
Próbowałem porównać zasięg rzutu z n obrotami koła, ale to do niczego nie doprowadziło
Wydaje mi się, że w punkcie a Całkowita prędkość jest V0 pionowa i V0 pozioma, więc kąt rzutu
powinnen się równać 45st.
Mam wrażenie , że trzeba uzależnić ilość obrotów koła od zasięgu.
Odpowiedzi podają wynik v0 = √πRg
Poproszę o jakąś wskazówkę i z góry dziękuję za pomoc
 Z jaką prędkością powinno toczyć się koło po poziomej powierzchni
, aby małe ciało, które oderwało się od tego koła z punktu A,
po przebyciu pewnej drogi w
powietrzu ponownie trafiło do
tego samego punktu na kole
po wykonaniu przez koło całkowitej liczby obrotów. Promień koła wynosi R.
(zb zadań Mendel, 245)
Próbowałem porównać zasięg rzutu z n obrotami koła, ale to do niczego nie doprowadziło
Wydaje mi się, że w punkcie a Całkowita prędkość jest V0 pionowa i V0 pozioma, więc kąt rzutu
powinnen się równać 45st.
Mam wrażenie , że trzeba uzależnić ilość obrotów koła od zasięgu.
Odpowiedzi podają wynik v0 = √πRg
Poproszę o jakąś wskazówkę i z góry dziękuję za pomoc
Z jaką prędkością powinno toczyć się koło po poziomej powierzchni
, aby małe ciało, które oderwało się od tego koła z punktu A,
po przebyciu pewnej drogi w
powietrzu ponownie trafiło do
tego samego punktu na kole
po wykonaniu przez koło całkowitej liczby obrotów. Promień koła wynosi R.
(zb zadań Mendel, 245)
Próbowałem porównać zasięg rzutu z n obrotami koła, ale to do niczego nie doprowadziło
Wydaje mi się, że w punkcie a Całkowita prędkość jest V0 pionowa i V0 pozioma, więc kąt rzutu
powinnen się równać 45st.
Mam wrażenie , że trzeba uzależnić ilość obrotów koła od zasięgu.
Odpowiedzi podają wynik v0 = √πRg
Poproszę o jakąś wskazówkę i z góry dziękuję za pomoc
22 sty 09:23
: Punkt A wykonuje ruch obrotowy i postępowy
vo =√2v, α = 45o
dalej już chyba prosto?
22 sty 10:14
aaaaaaaa: Wlasnie nie wiem, co dalej. Jak pisalem w pytaniu, ogarnalem, ze kat = 45 st
Nie widze jednak sensu opisywania V jako √2v , poniewaz mam obie predkosci skladowe(Vo),
Poniewaz i kolo, i rozpatrywane "male cialo" maja predkosc pozioma rowna V0, to jakakowliek by
nie byla,
Cialo zawsze "trafi" w kolo, jednak aby trafilo dokladnie w punkt A, kolo musi obrocic sie n
razy
Zatem myslalem na poczatku, ze musze rozpatrzyc rownanie
2πrx =( V02 * sin2a)/g
Ale szczerze mowiac niewiele mi to dalo, bo wprowadzilem x
Moze nadal czegos nie widze? Prosze o wskazowke
22 sty 12:11
aaaaaaaa: Właśnie ogarnąłem, że mogę spróbować wyliczyć x z drogi pionowej, bo obie prędkości są takie
same.
22 sty 12:16
: czas trwania rzutu ukośnego = wielokrotności okresu obrotu koła czyli nT, n= 1,2,3..
22 sty 14:08
aaaaaaaa: Tego też już próbowałem:
Wyszło mi tak =
T = 2πr / V0
n = (2sinaV0 / g ) / (2πr / V0) = (sina * V0 2 )/ gπr
potem próbowałem podstawić do równania
z = 2πr * x
(V02 * sin2a) /g = (2πr * sina * V0 2) / gπr
po skróceniu wyszło mi:
V02 sin2a = 2sinaV0
I tu przestałem liczyć, bo widać, że z tego nic nie wyciągnę.
Nie wiem, czy zrobiłem jakiś błąd rachunkowy, że mi nie wychodzi? Liczyłem parę razy
22 sty 14:39
:
http://fizyka.pisz.pl/strona/129.html
| 2vo sinα | 2v | |||
t = 2tw = | = | |||
| g | g |
22 sty 17:44
:
t = nT
v2 = nπRg
v= √nπRg
dla n= 1 ⇒ v = √πRg
| 2πR | ||
T = | ||
| v |
| 2v | 2πR | ||
=n | |||
| g | v |
22 sty 17:48
aaaaaaaa: Ach, dziękuje za za pomoc, nie wiem jakim cudem tyle mi to problemu sprawiało.
22 sty 18:21
aaaaaaaa: Jeszcze tylko mam jedno pytanie:
Odpowiedzi nie uwzgledniaja n, czy w takich zadaniach nalezy zalozyc najmniejsza niezerowa
wartosc,
czy to moze byc po prostu jakas literowka w ksiazce?
22 sty 18:55
aaaaaaaa: już nieważne, głupie pytanie, dziękuję jeszcze raz za pomoc
22 sty 20:02