Móglby ktos pomoc? z: Dwa jednakowe ładunki 𝑄=8∙10−7[𝐶] są umieszczone w odległości d =20cm od siebie. Na symetralnej odcinka łączącego ładunki, w odległości b =8cm od tego odcinka, rozpoczyna ruch elektron. Wyznaczyć maksymalną prędkość elektronu, którą nabędzie poruszając się w polu obu ładunków. Jak zmienia się siła działająca na elektron. Zapisz ostateczną postać wzoru na tę siłę.

luui: 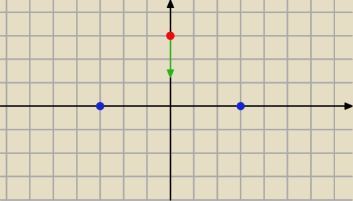W układzie kartezjańskim (ładunki Q leżą na osi OX, elektron w P(0, h) gdzie h=8cm:

	eQ
F= k		r
	||r3||

r = [−10 , −h] + [10 , −h] = [0, −2h] // superpozycja wektorów ||r|| = (100+h²)^(1/2) // odległość elektronu od ładunku (Q₁ i Q₂)

	eQ
F = −2hk
	(100+h2)(3/2)

	2hk	eQ
a = −
	me	(100+h2)(3/2)

dh		dv		2hk	eQ
	*		= −
dt		dh		me	(100+h2)(3/2)

	2hk	eQ
v dv = −			dh
	me	(100+h2)(3/2)

// maksimum funkcji wektorowej |a| dla h=0, chyba widać

v2		2hk	eQ
	= h∫0 (−			) dh
2		me	(100+h2)(3/2)

	4kQe		h
v = − [		0∫h (		) dh ]1/2
	me		(100+h2)(3/2)

	−1
całka =		0|0,08 = 3,2 * 10−6
	√h2+100

Zostało podstawić i gotowe.

luui: Każdą 100 zamień na 0,01... zapomniałem zamienić cm na m

z: Dziękuję za pomoc,ale czy dałoby się to zadanie zrobić w prostszy sposób bez całek,których jeszcze nie znam?

luui: Wartość siły będzie się zmieniać od położenia elektronu, więc chyba bez całki się nie obejdzie. Możliwe, że źle zinterpretowałem problem... pomyślę jeszcze jak skończę sprawozdanie i będę dostatecznie przytomny. Studia czy średnia?

z: Studia,ale jeszcze bez całek

korki_fizyka@tlen.pl: ale doktorat to już z całkami chyba?