fizyka.pisz.pl
forum zadankowe
matematyka w fizyce
kinematyka
dynamika
ruch obrotowy
pole grawitacyjne
teoria względności
siły sprężystości i drgania mechaniczne
fale mechaniczne
akustyka
elektrostatyka
prąd elektryczny
magnetyzm
indukcja i fale elektromagnetyczne
optyka
światło i atom
termodynamika
hydrostatyka
ciało stałe
przemiany jądrowe
gra w kropki
prędkość ciała przymocowanego do sprężyny
Jaehyo:
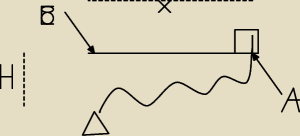 Ciało o masie m przymocowano do sprężyny, sprężynę rozciągnięto (obrazek).
Dane:
m=0.5kg
mi = 0.2
Ciało o masie m przymocowano do sprężyny, sprężynę rozciągnięto (obrazek).
Dane:
m=0.5kg
mi = 0.2
x=160cm
Obliczyć prędkość ciała w punkcie B.
zacząłem w ten sposób:
Δ Ek=W
EkA=0
W= (siła sprężystości) * x − mi*mg *x
i tu pojawia się problem, nie wiem jak zapisać poziome działanie tej siły sprężystości,
myślałem, że F=kx, ale z tego później jednostki się nie zgadzają.
Proszę o pomoc
 Ciało o masie m przymocowano do sprężyny, sprężynę rozciągnięto (obrazek).
Dane:
m=0.5kg
mi = 0.2
Ciało o masie m przymocowano do sprężyny, sprężynę rozciągnięto (obrazek).
Dane:
m=0.5kg
mi = 0.2
| N | ||
k=300 | ||
| m |
| mv2 | ||
EkB = | ||
| 2 |
9 cze 23:16
10 cze 10:11
Jaehyo: No tak, jak widać szukam pomocy na obu forach.
10 cze 14:23
jjj: Bez znanego H, chyba trudno będzie obliczyć końcową prędkość, na pewno nie ma jej podanej w
zadaniu?
10 cze 17:48
Jaehyo: nie mam nic zapisane co do H, ale pomijając już dokładne wartości, jak powinien wyglądać
schemat tego zadania?
jak zapisać tę siłę sprężystości?
10 cze 18:05
jjj: F1/F=x/√x2+H2 => F1=F*x/√x2+H2 , F=k√x2+H2 , więc F1=kx (F1) siła pozioma, więc
jak widać ta siła niezależy od H, trzeba pomyśleć co z prostopadłą bo ona też jest zmienna w
czasie,a więc i siła tarcia będzie zmienna.
10 cze 18:17
jjj: Masz może odp do tego zadania?
10 cze 19:32
Jaehyo: niestety nie mam odpowiedzi.
skoro ta pozioma siła F1=kx to ona nie zależy od niczego(czasu/drogi), tak?
o jaką prostopadłą chodzi?
skoro tarcie ma się zmieniać, to może jakaś całka? coś w stylu: 0x ∫ mi*m*g*s ds ?
10 cze 20:52
jjj: Chyba, że zadania jest łatwiejsze niż myśle i wystaczy po prostu ΔEk=1/2kx2−μmg*x. Choć ta
składowa siła sprężystości nie daje mi spokoju, im większe H tym i ona większa, a więc więcej
energii zostanie rozproszone przez tarcie.
10 cze 21:41
Jaehyo: Jeszcze podpytam, skąd się wzięła 1/2 przed kx2 ?
10 cze 22:33
jjj:
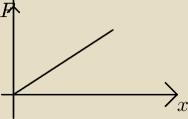 siła F jest proporcjonalna do rozciągniecia x, praca to pole pod wykresem, więc
W=kx*x*1/2=1/2kx2 i ta wykonana praca jest zmagazynowana w sprężynie jako energia potencjalna
siła F jest proporcjonalna do rozciągniecia x, praca to pole pod wykresem, więc
W=kx*x*1/2=1/2kx2 i ta wykonana praca jest zmagazynowana w sprężynie jako energia potencjalna
 siła F jest proporcjonalna do rozciągniecia x, praca to pole pod wykresem, więc
W=kx*x*1/2=1/2kx2 i ta wykonana praca jest zmagazynowana w sprężynie jako energia potencjalna
siła F jest proporcjonalna do rozciągniecia x, praca to pole pod wykresem, więc
W=kx*x*1/2=1/2kx2 i ta wykonana praca jest zmagazynowana w sprężynie jako energia potencjalna
10 cze 22:40
Jaehyo: faktycznie, to samo mi z całki wychodzi.
no dobra, dziękuję za wszelką pomoc
10 cze 22:50
: tak to jest jak się strzela z armaty do wróbla 

11 cze 09:22