Zasada zachowania momentu pędu Maslanek: Dwa pytania (przynajmniej na razie ): 1. Człowiek znajdujący się na krześle obrotowym obraca się z prędkością kątową ѡ. W wyciągniętych ramionach trzyma on dwa równe ciężarki. W pewnej chwili upuszcza te ciężarki nie zmieniając położenia rąk. Jak zmieni się (i czy zmieni się) prędkość kątowa? Czy prawo zachowania momentu pędu jest spełnione? Wyjaśnić to. 2. Człowiek idący po szynie kolejowej w pewnej chwili zaczyna tracić równowagę. W którą stronę wychyli on ciało w celu odzyskania równowagi, jeżeli zaczyna opadać w prawo? Wyjaśnić to. Do pierwszego zastosowałem doświadczenie (rzucanie książkami w domu podczas obrotu na krześle ). Moje obserwacje: prędkość kątowa po spuszczeniu książek maleje (drastycznie, biorąc pod uwagę, że myślałem, że się zwiększy ). Książka puszczona ląduje dalej od krzesła (nie spada pionowo w dół) Wnioski: na początku mamy tylko energię kinetyczną ruchu obrotowego. Potem energię kinetyczną ruchu obrotowego (ja na krześle) i kinetyczną ruchu postępowego (latająca książka). Czy można stosować zasadę zachowania momentu pędu? Wnioski i obserwacje pokazują, że nie. Dlaczego? Do drugiego − wychylamy się w tą samą stronę. Wydaje mi się, że zbliżamy oś obrotu do środka ciężko − mniejszy moment pędu. A następnie łapiemy równowagę korzystając z mięśni naszego ciała (w ten sposób równoważąc siłę grawitacji).

Piotr 10: p1 = p₂ I₁*ω₁ = I₂*ω₂ I₁ > I₂ ω₁ > ω₂ Więc wynika z tego, że nie można zastosować zasady zachowania momentu pędu, bo p₁≠p₂ Ale nie wiem czy to ok .

Maslanek: Nie można by stosować, kiedy działają siły zewnętrzne. Tutaj myślę, że chodzi raczej o siły wewnętrzne − znika napięcie mięśni, które mogły dawać moment pędu Ale to taka czysta hipoteza

Piotr 10: Aha, to poczekaj na kogoś innego

MQ: 1) Moim zdaniem moment pędu układu powinien być zachowany, bo jedyne siły, jakie działają na ciężarki, to siły ciężkości, a ponieważ ciężarki są takie same, więc ich momenty wzajemnie się równoważą. Gdyby nie były równe, to powstawał by pewien moment siły powodujący skręcenie osi obrotu. W momencie oderwania się ciężarków nie zmieniają się ich momenty pędu ani moment pędu poprzeczki ich łączącej, więc moment pędu całego układu też jest zachowany. Co do "gwałtownego" zwolnienia, to przypuszczam, że był on efektem sił oporu (głównie tarcia). Przedtem moment tych sił działał na układ o dużo większym momencie bezwładności, więc spowolnienie obrotu było mniejsze. Po odpadnięciu ciężarków działał tylko na układ o momencie bezwładności poprzeczki −− stąd jego efekty były bardziej widoczne. PS. Sorry, że nazwałem cię "poprzeczką"

daras: Jest to taka sama sytuacją jakby np. część bryły się urwała, zasadę zachowania stosujemy do całego układu ciał, zarówno przed jak i po upuszczeniu. Siły napięcia mięsni nic tu nie mają to są siły wewnętrzne.

MQ: Tak, tylko, że tutaj układ nie jest izolowany, bo działa na niego pole grawitacyjne. Na szczęście działa tak, że momenty sił ciężkości się znoszą. Zresztą moment pędu jest zachowany tylko do chwili upadku ciężarków na podłogę, ale tak daleko w przyszłość układacze tego zadania już chyba nie wychodzili

Maslanek: Więc w zasadzie prędkość kątowa nie powinna się zmienić? Przynajmniej tak długo jak nie działają siły tarcia? Jeżeli chodzi o dalszy stan rzeczy, to wraz z czasem moment pędu ciężarków powinien rosnąć (zwiększająca się odległość od krzesła, tego się nie da przeskoczyć ), a to by znaczyło, że również zasada zachowania momentu pędu nie mogłaby być spełniona (ja nie zmieniający swojego pędu w czasie i ciężarki, które swój pęd w czasie zmieniają). Coś tu nie gra Wybaczam poprzeczkę

MQ: 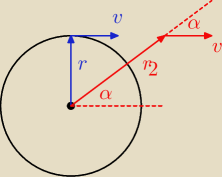Ad 1. Nie powinna. Ad 2. Moment pędu ciężarków nie rośnie, mimo że oddalają się od osi obrotu, patrz rysunek: moment pędu r^→×p^→=r^→×mv^→ W momencie oderwania kąt między r^→ a p^→ jest 90^o, czyli moment pędu jest L = rmv Po pewnym czasie, kąt jest α, więc L= r₂mvsinα

	r
ale		=sinα
	r2

stąd:

	r
L=r2mv		=rmv
	r2

Widzisz więc, że moment pędu się nie zmienia.

Maslanek: Bardzo fajne wyjaśnienie Teraz już rozumiem całkowicie zagadnienie A co z pytaniem numer 2? 2. Człowiek idący po szynie kolejowej w pewnej chwili zaczyna tracić równowagę. W którą stronę wychyli on ciało w celu odzyskania równowagi, jeżeli zaczyna opadać w prawo? Wyjaśnić to. Jak teraz czytam, to moje wyjasnienie tego pytania jest do niczego Na pewno wychyla się w tą samą stronę Wtedy też zmniejsza się kąt między siłą grawitacji a promieniem, więc moment siły maleje. To ma znowu wpływ na mniejszy przyrost momentu pędu w czasie. Co znowu daje większy czas na odpowiednią reakcję, spięcie mięśni, wyciągnięcie ręki w przeciwną stronę do ruchu itd.?

MQ: Z tym wychylaniem się w tę samą stronę, to nie do końca tak jest, bo rzeczywiście, wskutek utraty równowagi, ciało skręca w jedną stronę, ale my natychmiast skręcamy górną połowę ciała w drugą stronę. Daje to dwa efekty: 1. Przesuwa z powrotem położenie środka ciężkości nad szynę. 2. Powoduje powstanie momentu obrotowego przeciwdzałającego opadaniu ciała, po wychyleniu (niewielkim) środka ciężkości na drugą stronę. Dodatkowo dochodzą tu wyrzuty ramion i jednej nogi, które też zmieniają położenie środka ciężkości i moment pędu ciała, kompensujący ich moment pędu (zgodnie z zasadą zachowania momentu pędu). W obserwacji własnego chodzenia po równoważni człowiek skupia się psychicznie na wychyleniu ciała wskutek grawitacji, bo to czuje, i nie jest do końca świadomy, że te wychylenia sam konpensuje skrętami ciała w drugą stronę. Najlepiej więc poobserwować kogoś innego. Wtedy można obiektywnie coś zaobserwować. Poproś jakąś dziewczynę, żeby z tobą poeksperymentowała

Maslanek: Dzięki Od teraz przy takich wątpliwościach najpierw pojadę do dziewczyny i zaprowadzę ją na szyny Jak to mówią "skoro szyny są długie, to i stacja musi być bardzo fajna"