zadanie, sprawdzenie rozwiązania gość weselny: 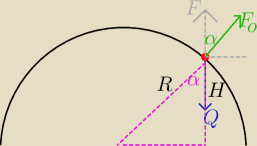Chłopiec, siedzący początkowo na szczycie bryły lodu w kształcie półkuli o promieniu R=13,8 m, zaczyna się ześlizgiwać się po lodzie. Jego prędkość początkowa równa jest zeru, a ruch odbywa się bez tarcia. Na jakiej wysokości nad odrywa się on od powierzchni bryły.To jest moja próba rozwiązania, więc tak napisałem najpierw warunek przy którym chłopiec się oderwie,czyli Fcosα=Fo. Po uproszczeniach wychodzi v²cosα/R=g. Cosinusa mogę też wyznaczyć jako H/R. Po podstawieniu wychodzi H=gR²/v². Zostało wyznaczyć prędkość, a ją można z z.z.e mgR=mgH + mv²/2, wyznaczmy v² i wstawiamy do wzoru i mamy równanie kwadratowe −2H²+2HR−R²=0. Dla danych w zadaniu danych szukana wysokość H równa jest około 3,7m. Czy takie rozwiązanie jest poprawne?

gość weselny: Cholera warunek dla równowagi sił to chyba jednak mv²cosα/r=mgcosα. Wtedy chyba wychodzi poprawnie H=1/2R

gość weselny: Oczywiście mv²/r=mgcosα, tak powinno być i wszystko ładnie wychodzi, głupie błędy wieczorową porą. Przepraszam i pozdrawiam

:

	2R
H =
	3