Środek ciężkości simon5005: 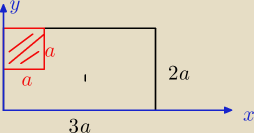Oblicz środek ciężkości układu składającego się z dwóch nałożonych na siebie płytek: prostokątnej i kwadratowej. Dane: a −> długość boku kwadratu M −> masa całego układu Czy to zadanie da się rozwiązać w ten sposób, że obliczam Sx i Sy (powierzchnia figury * współrzędna środka ciężkości) zarówno dla prostokąta jak i dla kwadrata potem dodaje je do siebie i dzielę przez powierzchnię prostokąta ? Byłyby to następujące obliczenia: prostokąt: Sy_p = 3a*2a*a = 6a³ Sx_p = 3a*2a*1,5a = 9a³ kwadrat: Sy_k = a*a*1,5a = 1,5a³ Sx_k = a*a*0,5a = 0,5 a³ Całość: Sy = 6a³ + 1,5a³ = 7,5 a³ Sx = 9a³ + 0,5a³ = 9,5 a³ A = 3a * 2a = 6a² yc = 7,5a³ / 6a² = 1,25 a xc = 9,5 a³ / 6a² = 1,58a Nie jest to chyba jednak prawidłowe rozwiązanie, jako A powinienem wziąć pole powierzchni prostokąta i kwadrata? O ile w ogóle ta metoda jest poprawna, jeśli nie jest proszę o nakierowanie na właściwe tory. Też w metodzie tej nie jest potrzebne M, które jest dane do zadania, z wykorzystaniem M trzeba by było to liczyć chyba poprzez całkowanie, proszę o odpowiedź czy mam rację.

: Potraktu prostokąt i kwadrat jako punkty materialne( ich środki mas znajdują się w środkach geometrycznych) i dalej wg definicji oddzielnie dla każdej składowej.