kinematyka nela: 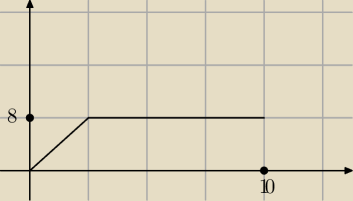Punkt materialny porusza się po linii prostej: przebywa drogę 67 m w czasie 10 s. Wykres przedstawia zależność wartości prędkości punktu od czasu. Oblicz czas w którym punkt materialny poruszał się ruchem jednostajnie przyspieszonym i oblicz wartość przyspieszenia z jakim poruszał się ten punkt do momentu osiągnięcia maksymalnej prędkości (8 m/s). Nie wiem jak rozwiązać to zadanie

: droga S = 67 m to pole pod wykresem szybkości reszta to czysta geometria

: pole trapezu(S) = pole trójkąta (S₁) + pole prostokąta(S₂)

	1
S1 =		vt, S2 = v(10−t)
	2

	Δv		8− 0		8
a =		=		=
	Δt		t−0		t

Leszek: S= 70 m , pole pod linia wykresu ! t₁ = 2,5 s , czas ruchu przyspieszonego ! a= 3,2 m/s² , przyspieszenie ruchu !

: Jakie 70 m przecież w treści zadania jest podane, że 67 m należy rozwiązać : 4t +8(10−t) = 67

	m
z tego t = 3,25 s , a ≈ 2,5
	s2

Leszek: Na podstawie wykresu S= 70 m , nalezy albo poprawnie napisac tresc , albo poprawie wykonac wykres , inaczej zadanie jest zle ! ! !

Google: właśnie takie jest to forum: zadający problem pisze abc, pomagający rozwiązują bca a chodziło od poczatku o cba