oporniki 280: 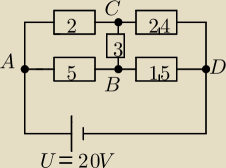Na rysunku powyżej przedstawiony jest schemat połączeń oporników o oporach 2Ω, 5Ω, 3Ω, 2,4Ω, 1,5Ω. Źródło napięcia 20V. Oblicz wartości natężeń prądów, płynących przez poszczególne oporniki. Doszedłem do momentu, w którym obliczyłem opór zastępczy całego układu, wyszedł mi 2,5Ω, z tego natężenie w głównym obwodzie to 8A. Nie wiem, co dalej zrobić. Proszę o podpowiedź

Lech: Trzeba rozwazyc trzy oczka sieci stosujac prawa Kirchhoffa ,troche jest pisania !

+-: Uważam, że prościej, trójkąt złożony z 2;3;5 zamienić na gwiazdę, jak obliczyłeś te 2,5Ω,

	5
mnie wychodzi 2		Ω
	7

280: Zmieniłem trójkąt 2 3 5 na gwiazdę. Możliwie ze u mnie bądź u ciebie, +−, wystąpił błąd w obliczeniach. Mnie jednak interesuje sposob obliczenia tj. co dalej zrobic z taka zamianą trójkąta na gwaizdę bo na tym stanąłem; a wynik − później się sprawdzi czy nie było błędu. Lech, spróbuję zrobić jak mówisz. Zobaczę czy mi wyjdzie, najwyżej poproszę o jeszcze jedna podpowiedź.

280: Ja widzę oczka 2Ω 2,4Ω i źródło napięcia 5Ω 1,5Ω i źródło napięcia 5Ω 3Ω 2,4Ω i ź.n. 2Ω 3Ω 1,5Ω ź.n. Ustaliłem ze prądy płynie w odcinku BC od C do B (w dol) Z drugiego prawa wyszło mi jedno równanie (dwa ale takie same) Z pierwszego prawa kirchhoffa mam trzy równania (przyjmując, że moje 8A to dobry wynik). Wynik nie chce mi wyjść proszę o pomoc.

280: Po prostu wyszło mi ze mam za mało danych żeby wyznaczyć te pięć prądów

+-: danych jest dość, narysuj jak to wygląda po zamianie to wytłumaczę, ja zmiast 1,5Ω spisałem 2,5Ω no i wtedy jest 2 5/7 , rzeczywiście zastępczy 2,5Ω, w gałeziach 2,4 i 1,5 płyną jednakowe prądy czyli 4A, spadki na 2,4 i 1,5 wyniosą odpowiednio 9,6V i 6V , z tego wynika spadek na 3Ω wynosi 3,6V czyli prąd 1,2A, przez 2Ω płynie (4+1,2)A, a przez 5Ω ( 4−1,2)A. Oczywiście z równań Kirchoffa musi wyjść to samo.

280: Dzięki juz biorę się do rysowania

280:

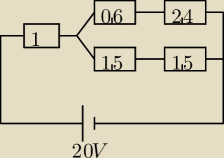
280: Aaaaa, już widzę, dziękuję bardzo za cierpliwość. Tak jak napisałeś: w dolnej i górnej popłyną te same prądy po 4A czyli przez 2,4 popłynie 4A i przez 1,5 popłynie 4A i spadki na tych opornikach wynoszą odpowiednio 9,6V i 6V, czyli prąd popłynie przez opornik 3Ω z natężeniem o wartości (9,6−6)V/3Ω = 1,2A, oczywiście z punktu C do B. Wtedy przez opornik 2omy popłynie prąd 4+1,2=5A a przez opornik 5omów popłynie prąd 4−1,2=2,8A. Czyli napisałem dokładnie to co ty, dziękuję jeszcze raz bardzo za pomoc, jestem bardzo wdzięczny.

280: Mam teraz pytanie, gdybyśmy chcieli rozwiązać za pomocą oczek, to jak te trzy oczka wyznaczyć?

280: Tzn, gdzie one są w tym przypadku?

+-: np. tak 1. 2I₁+2,4I₃=20 2. 5I₂+1,5I₄=20 3. 2I₁+3I₅−5I₂=0 4. I₄=I₂+I₅ 5. I₁=I₃+I₅ dalej wyznacznikami lub np. podstawiamy I₅ z 4. anastępnie I₁ z 5 i mamy. 4,4I₃+2I₄−2I₂=20 *5 1,5I₄+5I₂=20 *2 5I₄−10I₂+2I₃=0 8I₄+2I₃=40 5I₄+20I₃=100 75I₄=300 ⇒I₄=4 itd.

280: Dziękuję uprzejmie, faktycznie sposób z oczkami wydaje się trudniejszy głównie przez żmudne obliczenia i pięć niewiadomych. Jeszcze raz dziękuję.