Położenie centrum masy walca- wykres. ola11: 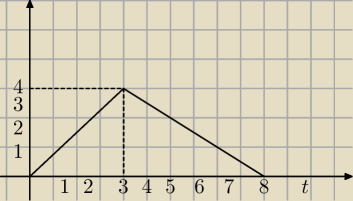Walec o promieniu R=0,5 m toczył się bez poślizgu po linii prostej. W chwili t0=0 jego centrum masy znajdowało się w położeniu x0=0. Wyznacz położenie centrum masy walca w chwili tk=8s. Do tego zadania jest też wykres omega(t), który opiszę: od 0s do 3 s wykres rośnie do omega=4 rad/s, następnie od 3s do 8s wykres maleje do omega=0. Proszę pomóżcie.

ω: v = rω x(t) = ∫₀^t v(t)dt + warunki początkowe

ola11: Nie miałam jeszcze całek

ω: to policz sobie pole

ω: albo podstaw ω_sr , która rośnie liniowo więc można bez całkowania

ola11: Pole pod wykresem wyszło 16, i to jest odpowiedź?

omega: przemyśl to jeszcze raz

omega: przemieszczenie (droga) to prędkość średnia razy czas najpierw prędkość rośnie a potem maleje...

omega: na mnie już czas dobranoc

ola11: x=v*t i v=ω*R x=ω*R*t3 −ω*R*t5= −4 tak ma być?