Układ w równowadze Mechanik: Wyznacz wartość kąta nachylenia α siły przyłożonej w punkcie P, w taki sposób aby układ był w równowadze w położeniu pokazanym na rysunku. Tarcza jest ciężka i jednorodna. Rysunek: https://zapodaj.net/images/3ae46429824a1.png

: ∑M_i = o ∑F_i = 0 rozwiąż

: w końcu to ty chcesz byc mechanikiem

'Leszek: Warunek rownowagi sil w kierunku pionowym : F*sin α = Q Warunek rownowagi momentow sil wzgledem punktu zaczepienia Q*a√2/2 * sin 45° = F a√2*sin (α +45°)

Mechanik: https://zapodaj.net/images/cb80b1151598a.png Czy chodzi o coś takiego? i teraz moment w punkcie A: (niech P oznacza siłę przyłożoną w punkcie P) ∑M_A = 0 P*a*cosα+P*a/2*sinα=0 cosα+1/2sinα=0 ∑F_x = 0 −R+P*sinα = 0 R = P*sinα ∑F_y = 0 −F+P*cosα = 0 F = P*cosα

Mechanik: 'Leszek, ale nie rozumiem skąd to 45°

Mechanik: Przecież nie znamy wartości kata

Mechanik: Powinno być odwrotnie chyba: ∑Fx = 0 −R+P*cosα = 0 R = P*cosα ∑Fy = 0 −F+P*sinα = 0 F = P*sinα

'Leszek: Zrob rysunek to zobaczysz ze kat miedzy ciezarem Q i przekatna kwadratu wynosi 45°, zas kat miedzy sila F i przekatna kwadratu wynosi ( α + 45°) przypomnij sobie definicje momentu sily: M_F = F*r*sin β, Z pierwszego rownania wyznacz F = Q/sin α ,podstaw do drugiego rownania i Wyznacz α

Mechanik: A co z siłą pochodzącą od podpory przesuwnej? (na moim rysunku oznaczonej jako "R")

'Leszek: A czy masz ja wyznaczyc , jezeli tak to R = P* cos α ( Twoje oznaczenia uzylem)

Mechanik: Przepraszam, ale kompletnie nie rozumiem Twojego sposobu rozwiązania, czy masz na myśli coś takiego? https://zapodaj.net/images/7d9cb33c0079d.png

Mechanik: sinα = 0, to nie będzie α = 0, przepraszam xd

Mechanik: sinα = 0, to nie będzie α = 90, przepraszam xd

'Leszek: Nie rozkladaj sily ciezaru ( u Ciebie F ) na skladowe !

Mechanik: wychodziłoby, że α=180

'Leszek: Suma momentow sil jest to suma algebraiczna , jeden moment jest dodatni , drugo ujemny wiec tam bedzie minus ( − ) !

Mechanik: Ok, załóżmy, że Q nie została rozłożona na składowe, więc, moment wzgl. B wynosi wtedy: ∑M_B = Q*1/2*a+F*a*cosα = 0 1/2Q + Fcosα = 0 [podstawiam F = Q/sin α − wcześniej podstawienie było błędne ^^']

	Q*cosα
1/2Q+		= 0
	sinα

1/2Q+Q*ctgα = 0 1/2 + ctgα = 0 ctgα = −1/2

Mechanik: Nie, chyba się poddaję...

'Leszek: Popatrz do podrecznika i dokladnie zapoznaj sie z definicja momentu sily ! ! M_F = F * r * sin β F − sila przylozona w danym punkcie r − odleglosc punktu przylozenia sily od osi obrotu bryly β − kat jaki tworzy wewktor sily F z odcinkiem r Moment sily ktory stara sie obrocic bryle przeciwnie do ruchu wskazowek zegara jest dodatni, drugi moment ktory stara sie obrocic bryle zgodnie z ruchem zegara jest ujemny , Czyli M₁ − M₂ = 0 ! ! !

Mechanik: Rozumiem, tylko, że dla mnie oba te momenty obracają bryłę w tym samym kierunku... na prawdę nie rozumiem, dlaczego jeden z nich miałby ją obracać w przeciwnym. Dla mnie oba momenty w punkcie są zgodne z ruchem wskazówek zegara.

Mechanik: Okej, ostatnie podejście. Momentu chyba już nie zrozumiem, więc próba z teorią trzech sił. Czy można to tu w ten sposób zastosować? https://zapodaj.net/images/815eb9c55a7e1.jpg

"Leszek: 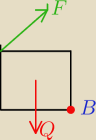weś kartę papieru wbij szpilkę w punkcie B i pociągnij kartę siłą w punkcie przyłożnie siły Q , kartka powinna się obrócić przeciwnie do ruchu wskazówek zegara, a następnie wchyć narożnik kartki w punkcie przyłożenia siły F , kartka powinna obrócić się przeciwnie !

Mechanik: 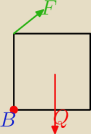Aaa, bo wcześniejszy moment liczyłem względem tego punktu:

"Leszek: rysunki techniczne musisz umieć czytaj i je poprawnie wykonywać, bez tego nie zrobisz poprawnie zadania !

Mechanik: Rozumiem, ale czy w takim razie, moje rozwiązanie jest jednak poprawne?

"Leszek: tgα =−2⇒ α = 116,56^o

"Leszek: twoje rozwiązanie na podstawie twierdzenia o trzech siłach jest poprawne ,ale masz błąd rachunkowy , tg β =1/2⇒ β = 26,56^o, czyli α = 116,56^o

Mechanik: Ok, widzę. Bardzo dziękuję za pomoc, teraz już wszystko rozumiem

: wbijanie szpilki w pkt. B nie jest zasadne w przypadku tego zadania, bo tam znajduje się podpora ślizgowa