Dynamika zadania Dragon502: 1). Do ciała o ciężarze P=5 kg uwiązano linkę, której drugi koniec trzymano w ręce. Jakie przyspieszenie a musi uzyskać ręka podnosząc pionowo ciało w górę, aby linka uległa zerwaniu? Siła rozrywająca linkę wynosi T=8.2 kg. P=mg m=P/g T=ma T=P/ga a=Tg/P a=8,2*9,81/5 a=16 [m/s²] 2). W kabinie maszyny dźwigowej ważymy dane ciało na wadze sprężynowej. Ciężar ciała wynosi P=10 kg, waga zaś wskazała R=11 kg. Znaleźć przyspieszenie a kabiny. P=mg m=P/g R=ma R=P/ga a=Rg/P a=11 * 9,81/10 a=10,79 [m/s²] 3). Obliczyć najmniejszą pracę, jaką należy wykonać, aby podnieść o L=3 m ciężar Q= 10 kg, ciągnąc go po równi pochyłej tworzącej z poziomem kąt α=30⁰. Współczynnik tarcia wynosi μ=0,2. Suma rzutów na oś x: −T+P−Qsinα=0 P− siła ciągnąca klocek do góry Suma rzutów na oś y: N−Qcosα=0 T=μN N=Qcosα T=μQcosα P=Qsinα+μQcosα=Q(μcosα+sinα) W=P*L W=Q(μcosα+sinα) *L W= 10(0,2*√3/2 + 1/2) *3 W=20,19 J 4). Wózek zjeżdża w polu grawitacyjnym po równi pochyłej z wysokości H, licząc od jej podstawy i wjeżdża na część kołową toru o promieniu R. Obliczyć prędkość wózka w górnym punkcie toru kołowego. Tarcie pominąć. Nie mam pomysłu 5). 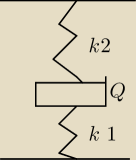Obliczyć okres drgań własnych ciężaru Q zamocowanego między dwoma zamocowanymi sprężynami o sztywnościach k₁ i k₂. Obliczyć sztywność zastępczą sprężyny równoważnej danemu układowi. Q=k₁x₁ Q=k₂x₂ Q=k(x₁+x₂) Q=k(Q/k₁+Q/k₂) 1/k=1/k₁+1/k₂ k=k₁k₂/(k₁+k₂) Prosiłbym o sprawdzenie. Pozdrawiam

'Leszek: zadanie 1) przede wszystkim masz bałagan z jednostkami , cieżar jest w [ N ] ( niuton) lub w [ kG ] ( kilogramsiła) 1 kG = 9,81 N przyspieszenie a = ( T − P)/m = ( 80,442 N − 49,09 N)/ 5 kg = 6,27 m/s² zadanie 2) P = 10 kG = 98,1 N R = 11 kG = 107,91 N R = P + ma ⇒ a= (R−P)/m = (107,91 N − 98,1 N)/10 kg = 0,98 m/s² , ruch kabiny w górę z przyspieszeniem lub w dół z opóznieniem zadanie 3) Dobrze zrobiłeś zadania 4) z zasady zachowania energii : mgH = mv²/2 + mg2R zadanie 5) napisz dokładnie jak zaczepiony jest ciężarek , czy sprężyny wiszą jedna pod drugą, czy obok siebie ?

Dragon502: 4). mgh=mv²/2 + mg2R /*2 2mgh = mv² + mg4R / :m 2gh=v²+g4R 2gh−v² = g4R −v² = −2gh−g4R v² = 2g(h−2R) v = √2g(h−2R) 5. Zapomniałem jeszcze okresu drgań policzyć: k=k₁k₂/(k₁+k₂) Q=mg m=Q/g ω²=k/m ω=√k/m ω=√kg/Q ω=√k₁k₂gQ/(k₁+k₂) T=2π/ω T=2π/√k₁k₂gQ/(k₁+k₂) T=2π√(k₁+k₂)/k₁k₂gQ

'Leszek: zadanie 5) @Dragon502 , Twoje rozwiązanie zadania 5) jest złe ! ruch harmoniczny nie wywołuje siła ciężaru Q ! siła sprężystości F₁ = k₁ x , F₂ = k₂ x siła wypadowa F = F₁ + F₂ = ( k₁ + k₂ ) x ma = −F ⇔ ma = − (k₁ + k₂ ) x czyli a = − ( k₁ + k₂ )*x/m porównanie z równaniem oscylatora harmonicznego : a = − ω²*x ⇒ ω² = ( k₁ + k₂ )/m⇒ T = 2π √ Q/g( k₁ + k₂ )