fizyka.pisz.pl
forum zadankowe
matematyka w fizyce
kinematyka
dynamika
ruch obrotowy
pole grawitacyjne
teoria względności
siły sprężystości i drgania mechaniczne
fale mechaniczne
akustyka
elektrostatyka
prąd elektryczny
magnetyzm
indukcja i fale elektromagnetyczne
optyka
światło i atom
termodynamika
hydrostatyka
ciało stałe
przemiany jądrowe
gra w kropki
Obbwody elektryczne
kot:
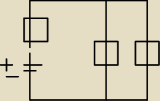 W obwodzie przedstawionym na rysunku wartość SEM jest stała, a opór R można zmieniać.
Znajdź wartość R dla której w tym oporniku wydziela się najwięcej energii termicznej.
Źródło jest doskonałe. Kolejno od lewej opornik R1 = 2 Ω R2= 5 Ω R3 można zmieniać
W obwodzie przedstawionym na rysunku wartość SEM jest stała, a opór R można zmieniać.
Znajdź wartość R dla której w tym oporniku wydziela się najwięcej energii termicznej.
Źródło jest doskonałe. Kolejno od lewej opornik R1 = 2 Ω R2= 5 Ω R3 można zmieniać
 W obwodzie przedstawionym na rysunku wartość SEM jest stała, a opór R można zmieniać.
Znajdź wartość R dla której w tym oporniku wydziela się najwięcej energii termicznej.
Źródło jest doskonałe. Kolejno od lewej opornik R1 = 2 Ω R2= 5 Ω R3 można zmieniać
W obwodzie przedstawionym na rysunku wartość SEM jest stała, a opór R można zmieniać.
Znajdź wartość R dla której w tym oporniku wydziela się najwięcej energii termicznej.
Źródło jest doskonałe. Kolejno od lewej opornik R1 = 2 Ω R2= 5 Ω R3 można zmieniać
28 lis 20:29
+-: Najprościej wyznaczyć zastępcze źródło napięciowe o szeregowej oporności oporności Rw
która będzie opornością zastępczą R1, R2 połączonych równolegle. Teraz Rw i R będą
połączone szeregowo wyznaczamy moc na R a następnie maxymum funkcji, choć z góry wiadomo,
| 10 | ||
że będzie to dla R=Rw= | Ω | |
| 7 |
28 lis 21:54
kot: Ale oporniki 1 i 2 nie są połączone równoległe, tylko opornik 2 i 3, ale po ich zmodyfikowaniu
beda
tworzyc z opornikiem 1 połączenie szeregowe. Ale jak to zapisać za pomocą różnicy potencjałów
(napięcia)?
U= R*I
I tu wypada te R skrócić, ale w rozwiązaniu zadania jest napisane że rożnica potencjałów jest
równa
I stąd moje pytanie, dlaczego tak jest?
| U2 | ||
P= | ||
| R |
| ε | ||
I= | ||
| R |
| R*ε | ||
U= | ||
| R |
| ε*R(rownoległe R2 i R3) | ||
U= | ||
| R(równolegle)+R1 |
28 lis 22:08
kot:
| 10 | ||
A jeszcze jedno pytanie, a skąd wiadomo że R=Rw= | Ω? | |
| 7 |
28 lis 22:16
+-: Obejrzyj Twierdzenie Thevenina.
Jeżeli nie będziesz mógł skorzystać z Twierdzenia Thevenina no to będzie trochę pisania.
Wyznaczasz Rz patrząc od źródła następnie Iź spadek na R1 odejmujesz od E i masz
napięcie na R ,P =U2/R i dalej maximum pochodna
28 lis 22:29
+-: Maksymalną moc uzyskuje się przy tzw. dopasowaniu czyli gdy oporność obciążenia jest
równa oporności wewnętrznej źródła. Jak to wyliczysz to zobaczysz,( możesz poczytać
o dopasowaniu).
.
28 lis 22:34