fizyka.pisz.pl
forum zadankowe
matematyka w fizyce
kinematyka
dynamika
ruch obrotowy
pole grawitacyjne
teoria względności
siły sprężystości i drgania mechaniczne
fale mechaniczne
akustyka
elektrostatyka
prąd elektryczny
magnetyzm
indukcja i fale elektromagnetyczne
optyka
światło i atom
termodynamika
hydrostatyka
ciało stałe
przemiany jądrowe
gra w kropki
Dwa walce na podwójnej równi pochyłej.
Licealistka:
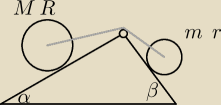 Dwa walce na podwójnej równi pochyłej:
Po dwóch stronach podwójnej równi pochyłej znajdują się dwa walce: jeden o masie M i promieniu
R, a drugi o masie m (m<M) i promieniu r (r<R). Walce mają tę samą wysokość d i są ze sobą
połączone nierozciągliwą nicią. Nić jest przyczepiona do osi walców u ich podstaw. Nić
przechodzi przez nieważki bloczek znajdujący się na szczycie równi pochyłej.
Oblicz przyspieszenie układu, jeśli współczynnik tarcia obu walców o powierzchnię równi wynosi
f. Walce poruszają się bez poślizgu.
Dwa walce na podwójnej równi pochyłej:
Po dwóch stronach podwójnej równi pochyłej znajdują się dwa walce: jeden o masie M i promieniu
R, a drugi o masie m (m<M) i promieniu r (r<R). Walce mają tę samą wysokość d i są ze sobą
połączone nierozciągliwą nicią. Nić jest przyczepiona do osi walców u ich podstaw. Nić
przechodzi przez nieważki bloczek znajdujący się na szczycie równi pochyłej.
Oblicz przyspieszenie układu, jeśli współczynnik tarcia obu walców o powierzchnię równi wynosi
f. Walce poruszają się bez poślizgu.
 Dwa walce na podwójnej równi pochyłej:
Po dwóch stronach podwójnej równi pochyłej znajdują się dwa walce: jeden o masie M i promieniu
R, a drugi o masie m (m<M) i promieniu r (r<R). Walce mają tę samą wysokość d i są ze sobą
połączone nierozciągliwą nicią. Nić jest przyczepiona do osi walców u ich podstaw. Nić
przechodzi przez nieważki bloczek znajdujący się na szczycie równi pochyłej.
Oblicz przyspieszenie układu, jeśli współczynnik tarcia obu walców o powierzchnię równi wynosi
f. Walce poruszają się bez poślizgu.
Dwa walce na podwójnej równi pochyłej:
Po dwóch stronach podwójnej równi pochyłej znajdują się dwa walce: jeden o masie M i promieniu
R, a drugi o masie m (m<M) i promieniu r (r<R). Walce mają tę samą wysokość d i są ze sobą
połączone nierozciągliwą nicią. Nić jest przyczepiona do osi walców u ich podstaw. Nić
przechodzi przez nieważki bloczek znajdujący się na szczycie równi pochyłej.
Oblicz przyspieszenie układu, jeśli współczynnik tarcia obu walców o powierzchnię równi wynosi
f. Walce poruszają się bez poślizgu.
27 maj 20:49
daras: Trzeba rozwiązać ukłąd r−ń:
(M + m) = Mgsinα − Mgfcosα − mgsinβ −mgfcosβ
i jeśli toczenie jest bez poślizgu to jeszcze
ε1R = ε2r
| 2 | ||
Mgfcosα = | ε1MR2 | |
| 3 |
| 2 | ||
mgfcosβ = | ε2mr2 | |
| 3 |
30 maj 10:36