fizyka.pisz.pl
forum zadankowe
matematyka w fizyce
kinematyka
dynamika
ruch obrotowy
pole grawitacyjne
teoria względności
siły sprężystości i drgania mechaniczne
fale mechaniczne
akustyka
elektrostatyka
prąd elektryczny
magnetyzm
indukcja i fale elektromagnetyczne
optyka
światło i atom
termodynamika
hydrostatyka
ciało stałe
przemiany jądrowe
gra w kropki
Elektrostatyka
herbatka:
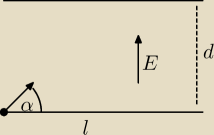 W obszar pola elektrycznego wpada pod kątem α = 45 st elektron poruszający się z
prędkością 6·106 m/s. Natężenie pola E = 2·103 N/C i jest skierowane do góry.
Odległość między płytkami d = 2 cm, a ich długość l = 10 cm. Czy elektron uderzy w
którąś z płytek? Jeżeli tak, to w którym miejscu?
W obszar pola elektrycznego wpada pod kątem α = 45 st elektron poruszający się z
prędkością 6·106 m/s. Natężenie pola E = 2·103 N/C i jest skierowane do góry.
Odległość między płytkami d = 2 cm, a ich długość l = 10 cm. Czy elektron uderzy w
którąś z płytek? Jeżeli tak, to w którym miejscu?
skorzystać, tylko pytanie jak wykorzystać to natężenie pola.
 W obszar pola elektrycznego wpada pod kątem α = 45 st elektron poruszający się z
prędkością 6·106 m/s. Natężenie pola E = 2·103 N/C i jest skierowane do góry.
Odległość między płytkami d = 2 cm, a ich długość l = 10 cm. Czy elektron uderzy w
którąś z płytek? Jeżeli tak, to w którym miejscu?
W obszar pola elektrycznego wpada pod kątem α = 45 st elektron poruszający się z
prędkością 6·106 m/s. Natężenie pola E = 2·103 N/C i jest skierowane do góry.
Odległość między płytkami d = 2 cm, a ich długość l = 10 cm. Czy elektron uderzy w
którąś z płytek? Jeżeli tak, to w którym miejscu?
| g | ||
Równanie paraboli rzutu ukośnego to y=(tgα)x − | x2 i pewnie z niego trzeba | |
| 2(V0 cosα)2 |
5 wrz 17:03
herbatka: Prędkość to 6·106 ms, a natężenie 2·103 NC. O gotowy wynik mi nie chodzi, ale gdyby
ktoś się czepiał. 

5 wrz 17:05
DeDe:
reszta tak jak w rzucie ukośnym
| F | ||
E= | , F =ma | |
| e |
5 wrz 20:28
herbatka: Dzięki! 

8 wrz 20:27
Olalalala: Hej, zrobiliście może to zadanie w całości? Nie rozumiem wciąż jak wykorzystać tam natężenie.
Proszę o pomoc!
18 mar 21:53
annabb: złożenie dwóch ruchów : w pionie jednostajnie zmienny, a w poziomie ruch jednostajny
zajmijmy się pionowym
siła która działa na ten elektron to F=E•e=ma i jest skierowana do dołu (bo E do góry to gdyby
był +)
i robi to samo co grawitacja jak rzucasz piłkę
więc ile czasu potrzeba by wlecieć na wysokość 2 cm = 0,002m
h= v0y•t−at2
(równanie kwadratowe ..delta itd...)
https://www.wolframalpha.com/input/?i=1.6*10%5E%28-19%29*1000%2F%289*10%5E%28-31%29%29*x%5E2-6*10%5E6*0.7071*x%2B0.002%3D0
t= 2,34•10−8
i ruch poziomy − jednostajny
więc w tym czasie przeleci w bok s=v0x•t= v•cosα•t = 9,8cm
czyli tuż przed końcem górnej okładki (2mm) uderzy płytkę
chyba żeby ktoś chciał się pobawić z większą precyzją 
| E•e | ||
0,002=v•sinα•t − | •t2 | |
| 2•m |

4 cze 21:28
korki_fizyka@tlen.pl: większej precyzji rachunkowej nie potrzeba ale przydały by się jednostki bo taki wynik jest do
dupy 

5 cze 09:08