fizyka.pisz.pl
forum zadankowe
matematyka w fizyce
kinematyka
dynamika
ruch obrotowy
pole grawitacyjne
teoria względności
siły sprężystości i drgania mechaniczne
fale mechaniczne
akustyka
elektrostatyka
prąd elektryczny
magnetyzm
indukcja i fale elektromagnetyczne
optyka
światło i atom
termodynamika
hydrostatyka
ciało stałe
przemiany jądrowe
gra w kropki
naczynie z cieczą
Leszek: Wyznaczyć równanie powierzchni swobodnej cieczy nielepkiej w naczyniu cylindrycznym
pionowym obracającym się wokół własnej osi środkowej z prędkością kątową ω .
21 cze 18:14
kawa: x2 + y2 = cz2
21 cze 22:36
Leszek: na postawie podanego równania wynika ,że ta powierzchnia jest stożkiem , a w
rzeczywistości jest to paraboloida obrotowa .
21 cze 22:51
Leszek:
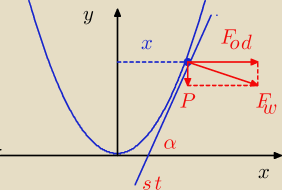
P=Δmg ; ciężar elementu cieczy
siła wypadkowa Fw j jest prostopadła do stycznej (st)
to jest równanie powierzchni cieczy w naczyniu

| Δmv2 | ||
Fod = | = Δmω2x ; siła odśrodkowa działająca na element Δm cieczy | |
| x |
| Fod | ω2x | |||
na podstawie rysunku tgα = | = | |||
| P | g |
| ω2x | ||
czyli dy/dx = tgα <=> dy/dx= | ||
| g |
| ω2x | ω2x | ω2 | ||||
zatem dy = | => y = ∫ | => y = | *x2 | |||
| g | g | 2g |
22 cze 12:18
Leszek:
| ω2x | ||
przy całce powinno być y= ∫ | dx | |
| g |
22 cze 12:19
Leszek: kurwa po co ja się wysilam, przecież to już napisali 5min przede mną

22 cze 15:15
Adam: korki .....
odczep się od p.Leszka , jesteś ........
22 cze 15:22