fizyka help me! ania13: hej! mam ogromne problemy z 2 zadaniam, z których prawdopodobnie będę pytana w piatek Ratujcie! Jedyna nadzieja w Was! 1. Zaprojektować instalację oświetleniową choinki włączoną do sieci o napięciu U = 220 V i złożoną z szeregowego połączenia jednej dużej żarówki o mocy P = 40 W i napięciu znamionowym U1 = 220V oraz kilkunastu żaróweczek latarkowych o napięciu znamionowym U2 = 3,8V i natężeniu I2 = 0,1A . Obliczyć niezbędną ilość żaróweczek n. Ma wyjsc n=26 tylko nie wiem jak do tego dojsc 2. Znaleźć wartość oporu R między punktami A i B prostokątnego obwodu o bokach a=1m i b=2m zrobionego z drutu stalowego o przekroju S = 1mm2. Oporność właściwa stali p=1,2∙10−7Ωm Z góry BARDZO dziękuje za pomoc

yht: Zad. 1 Instalacja choinkowa to połączenie szeregowe I₂=0.1A to maksymalny prąd jaki może przepłynąć przez żaróweczkę Jeśli popłynie większy, np. 0.11A to żaróweczka się spali Projektując instalację nie mogę dopuścić żeby przepłynął prąd większy niż 0,1A Obliczam maksymalny prąd jaki może przepłynąć przez dużą żarówkę bo może się okazać że duża żarówka może nie wytrzymać nawet prądu 0,1A P₁ = 40W U₁=U₁ = 220V I₁ = ? P = U*I P₁ = U₁*I₁ |:U₁

P1
	= I1
U1

40W
	= I1
220V

	2
I1 =		A ≈ 0.18 A
	11

	2
Duża żarówka jest w stanie wytrzymać prąd		A czyli ok. 0.18A
	11

Więc najsłabszym elementem pozostają małe żaróweczki, które wytrzymują prąd do 0.1A Przyjmujemy, że I_max = 0.1A Z prawa Ohma obliczam maksymalny opór R_max, który może wytrzymać projektowana instalacja:

	U
Rmax =
	Imax

	220V
Rmax =
	0.1A

R_max = 2200Ω Opór zastępczy R_Z w połączeniu szeregowym jest sumą oporów poszczególnych elementów (u nas tymi elementami będą żaróweczki): R_Z = R_a + R_b + R_c + R_d + R_e + ..... Obliczam opór dużej żarówki z prawa Ohma:

	U1
R1 =
	I1

	220V
R1 =
	2   A 11

	11
R1 = 220*		Ω
	2

R₁ = 1210 Ω Obliczam opór jednej małej żaróweczki

	U2
R2 =
	I2

	3.8V
R2 =
	0.1A

R₂ = 38Ω Mamy jeden element R₁, oraz n elementów R₂ Suma oporów tych elementów, czyli R₁ + n*R₂, musi być większa niż wartość oporu zastępczego R_Z = 2200Ω Układamy nierówność i ją rozwiązujemy: R₁ + R₂*n > R_Z 1210 + 38n > 2200 38n > 2200−1210 38n > 990 |:38

	990
n >
	38

n > 26,05.... Czyli możemy wziąć 26 małych żaróweczek do instalacji *** Warto w tym miejscu wyjaśnić fakt, dlaczego spalenie się jednej żaróweczki powoduje lawinowe spalanie się kolejnych Załóżmy że w instalacji spaliła się jedna mała żaróweczka, czyli została 1 duża żarówka i 25 małych Policzmy opór zastępczy R_Z całego układu, składającego się z 1 dużej i 25 małych żaróweczek: R_Z = 1210Ω + 25*38Ω R_Z = 1210Ω + 950Ω R_Z = 2160Ω

	U
Policzmy teraz prąd, jaki płynie w całym układzie, ze wzoru I =		, który to wzór wynika z
	R

przekształconego wzoru na prawo Ohma

	U
I =
	RZ

	220V
I =
	2160Ω

I ≈ 0.10185185185 A Czyli prąd w układzie wyszedł większy niż 0,1A a żaróweczki są dostosowane tylko do prądu co najwyżej 0,1A więc się szybko spalą im więcej żaróweczek się spali, tym mniejsza wartość R_Z oraz większa wartość I Zad. 2

	L
Wzór: R = p*
	S

p = 1.2*10⁻⁷ Ωm L = obwód prostokąta S = 1mm² L = 2a+2b L = 2*1+2*2 L = 2+4 L = 6m

	6m
R = 1.2*10−7 Ωm *
	1mm2

Jednostki muszą się zgadzać, więc w tym S = 1mm² warto zamienić milimetry na metry: 1 mm² = 1mm*1mm = 0,1cm*0,1cm = 0,1*0,01m * 0,1*0,01m = 0,001m*0,001m = 0,000001 m² = 10⁻⁶ m²

	6m
R = 1.2*10−7 Ωm *
	10−6 m2

	10−7
R = 1.2*6*		Ω
	10−6

R = 7.2 * 10^{−7−(−6)} Ω R = 7.2 * 10⁻⁷⁺⁶ Ω R = 7.2 * 10⁻¹ Ω R = 7.2 * 0,1 Ω R = 0.72 Ω

ania13: Mega dziękuję za 1 zadanie To czemu ja mam w odpowiedzi inny wynik? R=pa(a+2b)/2S(a+b)

yht: Szczerze mówiąc − nie mam pojęcia.. A był jakiś rysunek do tego zad. 2 ?

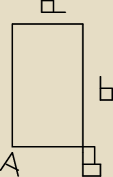madzia11: podpisany tylko boki a i b oraz naroznik A i B