fizyka.pisz.pl
forum zadankowe
matematyka w fizyce
kinematyka
dynamika
ruch obrotowy
pole grawitacyjne
teoria względności
siły sprężystości i drgania mechaniczne
fale mechaniczne
akustyka
elektrostatyka
prąd elektryczny
magnetyzm
indukcja i fale elektromagnetyczne
optyka
światło i atom
termodynamika
hydrostatyka
ciało stałe
przemiany jądrowe
gra w kropki
Kąt
rick:
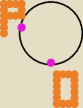 Czy wie ktoś, w jaki sposób obliczyć kąt nachylenia punktu P do podłoża, wiedząc, że znajduje
się on na brzegu okręgu, a jego szybkość liniowa wyraża się wzorem: √10/3gR, a szybkość
liniowa punktu O: √2/3gR ?
Proszę o pomoc !
Czy wie ktoś, w jaki sposób obliczyć kąt nachylenia punktu P do podłoża, wiedząc, że znajduje
się on na brzegu okręgu, a jego szybkość liniowa wyraża się wzorem: √10/3gR, a szybkość
liniowa punktu O: √2/3gR ?
Proszę o pomoc !
 Czy wie ktoś, w jaki sposób obliczyć kąt nachylenia punktu P do podłoża, wiedząc, że znajduje
się on na brzegu okręgu, a jego szybkość liniowa wyraża się wzorem: √10/3gR, a szybkość
liniowa punktu O: √2/3gR ?
Proszę o pomoc !
Czy wie ktoś, w jaki sposób obliczyć kąt nachylenia punktu P do podłoża, wiedząc, że znajduje
się on na brzegu okręgu, a jego szybkość liniowa wyraża się wzorem: √10/3gR, a szybkość
liniowa punktu O: √2/3gR ?
Proszę o pomoc !
7 maj 17:51
MQ: Co to za pojęcie "szybkość liniowa"?
Co oznaczają wielkości g i R?
7 maj 18:24
MQ: Poza tym, jaka jest fizyka tego ruchu?
1. Czy okrąg się toczy, czy ślizga?
2. Czy p. P jest sztywny na okręgu, czy ślizga się po okręgu?
3. Pod wpływem czego występuje ruch p. P?
7 maj 18:27
rick:
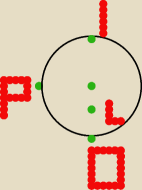 Oto dokładny rysunek :
Płaską jednorodną tarczę o promieniu R umocowano zaczepem w pozycji pionowej na gwoździu wbitym
w ścianę w punkcie L, jak pokazuje rysunek. Po usunięciu zaczepu tarcza opuszcza położenie
równowagi nietrwałej z prędkością początkową równą zeru.
Odległość między środkiem tarczy,a punktem L wynosi R/2.
Szybkość liniowa punktu P: √10/3gR
Oblicz kąt, jaki prędkość Vp tworzy z poziomem.
Oto dokładny rysunek :
Płaską jednorodną tarczę o promieniu R umocowano zaczepem w pozycji pionowej na gwoździu wbitym
w ścianę w punkcie L, jak pokazuje rysunek. Po usunięciu zaczepu tarcza opuszcza położenie
równowagi nietrwałej z prędkością początkową równą zeru.
Odległość między środkiem tarczy,a punktem L wynosi R/2.
Szybkość liniowa punktu P: √10/3gR
Oblicz kąt, jaki prędkość Vp tworzy z poziomem.
 Oto dokładny rysunek :
Płaską jednorodną tarczę o promieniu R umocowano zaczepem w pozycji pionowej na gwoździu wbitym
w ścianę w punkcie L, jak pokazuje rysunek. Po usunięciu zaczepu tarcza opuszcza położenie
równowagi nietrwałej z prędkością początkową równą zeru.
Odległość między środkiem tarczy,a punktem L wynosi R/2.
Szybkość liniowa punktu P: √10/3gR
Oblicz kąt, jaki prędkość Vp tworzy z poziomem.
Oto dokładny rysunek :
Płaską jednorodną tarczę o promieniu R umocowano zaczepem w pozycji pionowej na gwoździu wbitym
w ścianę w punkcie L, jak pokazuje rysunek. Po usunięciu zaczepu tarcza opuszcza położenie
równowagi nietrwałej z prędkością początkową równą zeru.
Odległość między środkiem tarczy,a punktem L wynosi R/2.
Szybkość liniowa punktu P: √10/3gR
Oblicz kąt, jaki prędkość Vp tworzy z poziomem.
7 maj 18:39
MQ: Wychodząc z równania ruchu dla wahadła fizycznego:
Iε=M, gdzie ε to przyspieszenie kątowe
dostajesz równanie na kąt α odchylenia p. O
Ale nas interesuje zależność prędkości kątowej ω od α, więc przekształcamy to równanie na:
Dla warunku początkowego: α=0, ω=0
Jeśli się gdzieś nie walnąłem, to rozwiązaniem jest:
ω=2√g/R(1−cos(α))
Nas interesuje prędkość liniowa, więc:
vO=ωR/2=√gR(1−cos(α)) dla p. O oraz
vP=ωR√3/2=√3gR(1−cos(α))
α jest równy, jaki vO tworzy z poziomem, więc z geometrii problemu wynika, że kąt dla vP
Podstawiając za vP podaną wartość, wyliczysz sobie α, a potem φ
| d2α | 2g | ||
= | sin(α) | ||
| dt2 | R |
| dω | 2g | ||
ω= | sin(α) | ||
| dα | R |
| 2π | ||
kąt wektora prędkości z poziomem wynosi φ=α− | ||
| 3 |
7 maj 21:37
MQ: Jakiś bełkot mi wyszedł pod koniec, więc poprawki:
4 linia od końca: brakuje dopisku "dla p. P"
3 linia od końca powinna brzmieć:
kąt α jest równy kątowi, jaki vO tworzy z poziomem, więc z geometrii problemu wynika, że dla
vP
7 maj 21:41
rick: Dziękuję za pomoc  Poradziłem sobie z pozostałymi podpunktami zadania, jednakże tego z pewnością bym nie zrobił,
ponieważ nie omawiałem jeszcze wahadła.
Pozdrawiam !
Poradziłem sobie z pozostałymi podpunktami zadania, jednakże tego z pewnością bym nie zrobił,
ponieważ nie omawiałem jeszcze wahadła.
Pozdrawiam !
 Poradziłem sobie z pozostałymi podpunktami zadania, jednakże tego z pewnością bym nie zrobił,
ponieważ nie omawiałem jeszcze wahadła.
Pozdrawiam !
Poradziłem sobie z pozostałymi podpunktami zadania, jednakże tego z pewnością bym nie zrobił,
ponieważ nie omawiałem jeszcze wahadła.
Pozdrawiam !
7 maj 21:56