Samochód w wesołym miasteczku Rafał: 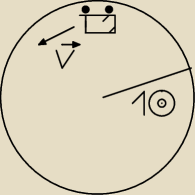Samochód w wesołym miasteczku o masie m porusza się po poziomym torze z pewną prędkością v₀. Pokonuje pionowo utawioną pętlę o promieniu R=10m. Narysuj siły działające na samochód w

	km
najwyższym punkcie pętli. Oblicz minimalną szybkość w		z jaka samochód powinien
	h

wjechać na pętle, aby mógł ją bezpiecznie pokonać. Pomiń tarcie i opór ruchów.

	km
Odpowiedz to ok 80
	h

Wiem że to z zasady zachowanie Energii E_k=E_p Ale coś jeszcze tutaj trzeba, bo taki wynik nie wychodzi

MQ: W najwyższym punkcie: Siła odśrodkowa ≥ ciężaru samochodu

Rafał:

	mv2
Siłą odśrodkową możemy wyrazić wzorem F=		ciężar Q= m*g to jak podstawimy to do tego
	R

co napisałeś nie wychodzi prędkość taka jaka powinna wyjść. Mógłby ktoś rozwiązać to zadanie ?

axxy: mi wychodzi około 72km/h, jak z z.z.e to będziesz miał v=√2gh, h=2r i potem zamienisz z m/s −> km/h

Saizou : na pewno odp. to 80 km/h≈22 m/s ?

Rafał: Widocznie w odpowiedziach jest błąd bo z tego co piszecie to:

	mv2
1. z zasady zachowania energii		=mgh to wtedy h= 72 km/h
	2

	mv2
2. Jak z Siła odśrodkowa ≥ cięzar samochodu to		≥ mg to wtedy v=36 km/h
	R

Wydaje mi się że pierwszy sposób jest dobry..

daras: Jeśli traktujemy samochód jako punkt a nie bryłę, to E_ko = E_K +E_p. w najwyższym punkcie punkcie toru samochór powinien mieć niezerowa predkość, aby nie spaść ale pytanie jest o to jaką musi mieć prędkość na dole, przy wjeżdżaniu na petlę żeby się tam w ogóle dostać więc:

mVo2		mV2
	= mgh +		, gdzie h = 2R a v = √gR.
2		2

	m		km
ostatecznie vo = √5gR ≈ 22,4		= 80,5		.
	s		h

Rafał: Dzięki wielkie Daras

daras: