Wykres przedstawia zależność prędkości rowerzysty od czasu w pierwszych sekundac john2: 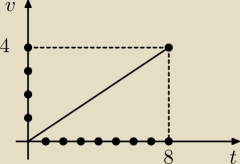Wykres przedstawia zależność prędkości rowerzysty od czasu w pierwszych sekundach ruchu. Jaką energię kinetyczną uzyskał kolarz po 8 s, jeżeli jego masa wynosi 70 kg, a masa roweru to 10 kg? Moje pytanie dotyczy treści zadania. Czy jest jednoznacznie określone, o które 8 sekund chodzi, czy jest to kwestia interpretacji? W książce odpowiedź to E = 2560 J, bo, jak rozumiem, chodzi im o kolejne 8 sekund ruchu (nie pierwsze 8). Jeśli chodzi o pierwsze 8 sekund ruchu, to wyjdzie 640 J. Drugie pytanie: Czy nie jest też sporną kwestią, jaką masę podstawić we wzorze? Pytanie jest o energię kolarza, czyli człowieka ważącego 70 kg, a nie o energię człowieka i roweru.

daras: Jest wyraźnie napisane "po ośmiu sekundach"

daras: Pytanie jest absurdalne przecież wykres jest tylko dla tych pierwszych 8 sek gdyby to był wykres powiedzmy minutowy, godzinny..to zrozumiałbym Twoje wątpliwości Pyt.2 nie ma żadnych wątpliwości przecież rower nie jedzie osobno z inna szybkością niz rowerzysta, który na nim siedzi

daras: PS. nie da sie niczego policzyć , bo na wykresie nie ma jednostek

john2:

	m
Zapomniałem o jednostkach. Prędkość jest podana w		, zaś czas w sekundach.
	s

Czyli, która odpowiedź jest poprawna − ta z książki czy moja? Jest wyraźnie napisane "po ośmiu sekundach". Zgadza się. Tylko czy mówimy o pierwszych ośmiu sekundach (0:00 − 8:00 na stoperze), czy o kolejnych ośmiu sekundach (8:00 − 16:00 na stoperze). Dla mnie, patrząc na ten wykres, logiczne wydaje się, że chodzi o przyrost energii, który nastąpił w pierwszych ośmiu sekundach ruchu.

	mv2		m   80 kg * (4 )2   s
Ek =		=		= 640 J
	2		2

Odpowiedź z książki sugeruje, że obliczenia wykonane zostały dla kolejnych 8 sekund, w trakcie

	m
których nastąpił przyrost prędkości o kolejne 4 metry na sekundę (w sumie 8		).
	s

	mv2		m   80 kg * (8 )2   s
Ek =		=		= 2560 J
	2		2

Kwestia druga: Nie twierdzę, że rower jedzie z inną szybkością.

	m
Oczywiście człowiek osiąga prędkość dzięki rowerowi. Osiąga prędkość 4		.
	s

I rower i człowiek mają tę samą prędkość i jako całość mają energię E = 640 J albo 2560 J (w końcu nie wiem). Ale przecież można spojrzeć na energię człowieka w odosobnieniu od źródła prędkości, którym jest rower (powiedzmy, że to lecący superman).

	masa roweru (10 kg) * prędkość roweru
Energia roweru to wtedy		.
	2

Energia człowieka to

masa człowieka (70 kg) * prędkość człowieka (nie ważne, dzięki czemu uzyskana)
	.
2

	masa roweru+człowieka (80 kg) * prędkość roweru i człowieka
Energia całego układu
	2

john2: Jeszcze odnośnie do kwestii nr 1. Moja interpretacja odpowiedzi z książki jednak, nie wiem, czy jest fortunna. Przyrost energii w kolejnych ośmiu sekundach byłby taki sam jak w pierwszych ośmiu sekundach, bo mamy ten sam przyrost prędkości.

	m
Zatem wstawiając do wzoru 8		to tak, jakby liczyć przyrost prędkości w pierwszych 16
	s

sekundach. Nie rozumiem zatem, skąd ta odpowiedź 2560 J.

john2: miałem napisać "to tak, jakby liczyć przyrost energii w pierwszych 16 sekundach"

daras: Przecież z wykresu nie wiemy jak poruszał się rower po ósmej sekundzie więc nie wiem o co kaman:(

john2: Domyślam się, że rośnie prędkość tak samo i po 16 sekundach osiąga wartość 8 m/s, ale no w zasadzie, skąd to wiadomo. Uznaję odpowiedź z książki za niepoprawną w takim razie.

daras: Domyślasz się ...a na jakiej niby podstawie To sa teorie spiskowe wg mnie odpowiedź na pytanie: jaką E_k uzyskał kolarz po ośmiu sekundach brzmi: 640 J i koniec, kropka .

john2: Zgoda, a druga kwestia? Ma to sens, co piszę? Gdyby wziąć pod uwagę tylko kolarza (bez roweru), to ma on energię?

john2: czy ma energię kinetyczną*