fizyka.pisz.pl
forum zadankowe
matematyka w fizyce
kinematyka
dynamika
ruch obrotowy
pole grawitacyjne
teoria względności
siły sprężystości i drgania mechaniczne
fale mechaniczne
akustyka
elektrostatyka
prąd elektryczny
magnetyzm
indukcja i fale elektromagnetyczne
optyka
światło i atom
termodynamika
hydrostatyka
ciało stałe
przemiany jądrowe
gra w kropki
.
Rysiu:
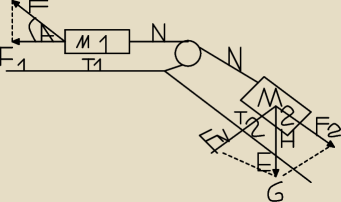 Witam mam takie zadanie. Oblicz przyśpieszenie układu mas i znajdź naprężenie linek.
Przepraszam za mało czytelny rysunek.
Q1− kinetyczny współczynnik tarcia dla masy M1
Q2−kinetyczny współczynnik tarcia dla masy M2
F− dodatkowa siła przyłożona do masy M1
E i H− kąty
reszta chyba powinna być jasna.
Więc robię to zadnie w ten sposób.
F1−T1−N=M1a
N−F2−T2=M2a
Witam mam takie zadanie. Oblicz przyśpieszenie układu mas i znajdź naprężenie linek.
Przepraszam za mało czytelny rysunek.
Q1− kinetyczny współczynnik tarcia dla masy M1
Q2−kinetyczny współczynnik tarcia dla masy M2
F− dodatkowa siła przyłożona do masy M1
E i H− kąty
reszta chyba powinna być jasna.
Więc robię to zadnie w ten sposób.
F1−T1−N=M1a
N−F2−T2=M2a
F1=cosA*F
T1=Q1*M1g
Fn=sinE*M2*g
T2=Fn*Q2
F2=cosH*m2*g
tutaj juz zostaje tylko podstawienie do wzorów i wyliczenie N i a. Mam nadzieję że to jest
dobrzę. Ale miałbym kłopot co zrobić w razie gdyby ta "dodatkowa" siła F była przyłożona w
inny sposób np. przyłożona do M2 równolegle do równi pochyłej lub prostopadle do równi. Bardzo
proszę o sprawdzenie i ewentualne wskazówki co zrobić gdyby ta siła była przyłożona w inny
sposób.
 Witam mam takie zadanie. Oblicz przyśpieszenie układu mas i znajdź naprężenie linek.
Przepraszam za mało czytelny rysunek.
Q1− kinetyczny współczynnik tarcia dla masy M1
Q2−kinetyczny współczynnik tarcia dla masy M2
F− dodatkowa siła przyłożona do masy M1
E i H− kąty
reszta chyba powinna być jasna.
Więc robię to zadnie w ten sposób.
F1−T1−N=M1a
N−F2−T2=M2a
Witam mam takie zadanie. Oblicz przyśpieszenie układu mas i znajdź naprężenie linek.
Przepraszam za mało czytelny rysunek.
Q1− kinetyczny współczynnik tarcia dla masy M1
Q2−kinetyczny współczynnik tarcia dla masy M2
F− dodatkowa siła przyłożona do masy M1
E i H− kąty
reszta chyba powinna być jasna.
Więc robię to zadnie w ten sposób.
F1−T1−N=M1a
N−F2−T2=M2a
| F1 | ||
cosA= | ||
| F |
| Fn | ||
sinE= | ||
| M2*g |
| F2 | ||
cosH= | ||
| M2*g |
2 lip 18:29
qwark: Drogi kolego Rysiu!
skoro sie nie przyłożyłeś nawet żeby pooznaczać wielkości odpowiednimi symbolami, które masz w
pasku tuż nad polem tekstu, to...
3 lip 14:09
qwark: Q−1 , Q−2 − to siły ciężkości
3 lip 14:10
qwark: a współczynniki tarcia to odpowiednio: μ1 , μ2
3 lip 14:10
qwark: kąty: α, β
itd.
3 lip 14:12
qwark: przy czym o ile dobrze odczytuje twój rysunek, to źle oznaczyłeś ∡β −nachylenia zbocza, gdzie
siła nacisku jest zawsze równa m2gcosβ
3 lip 14:15
qwark: Poza tym dałeś się złapać na drugi częsty błąd w takich przypadkach.
Pominąłeś drugą składową siły F, tę pionową, która zmniejsza nacisk masy m1: F⊥ = Fsinα
więc r−nie ruchu powinno mieć postać:
Fw = (m1 + m2)a = Fcosα −μ1(m1g − Fsinα) − m2gsinβ − μ2m2gcosβ
3 lip 14:20
qwark: reszta chyba powinna być jasna  a gdyby dodatkowa siła była przyłożona w innym miejscu, to zawsze postępujesz w ten sam sposób
a gdyby dodatkowa siła była przyłożona w innym miejscu, to zawsze postępujesz w ten sam sposób
 a gdyby dodatkowa siła była przyłożona w innym miejscu, to zawsze postępujesz w ten sam sposób
a gdyby dodatkowa siła była przyłożona w innym miejscu, to zawsze postępujesz w ten sam sposób
3 lip 14:22