układ nieruchomych ładunków blackapple: 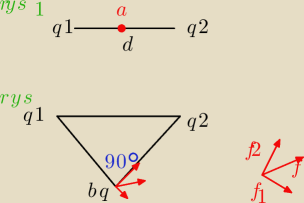Dany jest układ nieruchomych ładunków przedstawiony na rysunku 1: W którym q1= +q, q2=−2q, d − odległość między ładunkami. a) Gdzie natężenie pola wynosi 0 Chciałam to obliczyć tak, że a − punkt w którym natężenie wynosi 0 w tym punkcie: k*q1/a²=k*q2/(d−a)² q1(d−a)²=q2*a² q1(d−a)²−q2a²=0 q1−q2[(d−a)²+a²]=0 q1−q2[d²−2da+a²+a²]=0 i tu się pogubiłam, bo nie wiem co mam zrobić z tym, że w tym równaniu zarówno d jaki i a są popodniesione do kwadratu? Czy przyjąć, że d to jakaś liczba, a a pełni funkcję taką jak x w równaniach kwadratowych? Czy wymnaża to potem przez q1−q2? Jak podstawić potem wartości tych ładunków? b) Gdzie potencjał pola wyniesie 0? Czy to będzie coś takiego?: 0=V1+V2=k*q1/d+k*q2/d= k(q1+q2)/d Jeśli tak, to co z tym dalej? c) Jaka siła działałaby na dodatkowy ładunek umiejscowiony w punkcie b (rysunek 2), o wartości q3= +q Siły rozrysowałam na czerwono. Wnioskuję, że wówczas, między f1 a f2 również będzię 90, czyli między f1 a f 45 stopni. f1=k*q1*q3/d²=k*q²/d² f2=k*q2*q3/d² f1/f2=sin45 f1/f2=√2/2 => q1q2=√2/2 jak tu podstawić wartości ładunków skoro jeden jest ujemny? Czy w ogóle ten tok myślenia jest poprawny?

korki_fizyka@o2.pl: 1. punkt A (punkty oznaczamy wielkimi literami) musi znajdować się bliżej ładunku q₁ , tego o mniejszej wartości bezwzględnej, dalej dobrze zaczęłaś , aby się pozbyć kwadratów należy spierwiastkować, gubi się przy tym drugi, ujemny pierwiastek ale od czego jest głowa? należy zinterpretować otrzymany wynik− natężenia są wektorami a ty zapisałaś r−nie skalarne stąd 2 pierwiastki 2. potencjały sa skalarami więc nie będzie z nimi takiego problemu jak z wektorami natężeń, wystarczy poszukać sumy algebraicznej uwzględniając przy tym znaki ładunków 3. siły narysowałaś dobrze a skoro w wierzchołku jest kąt prosty, to wystarczy zastosować tw. Pitagorasa

korki_fizyka@o2.pl: ad. 3 podstaw wartości bezwzględne ładunków, przecież ich znaki już uwzględniłaś przy rysowaniu zwrotów sił