Ruchoma równia i klocek Anka: Ruchoma równia i klocek Mam zadanie, które dosłownie zabiło mnie na egzaminie, więc bardzo proszę o wyjaśniecie. Między równią o masie M, a podłożem oraz miedzy klockiem o masie m na równi i równią nie ma tarcia. Klocek zsuwa się z równi, pod wpływem czego równia odjeżdza przeciwnie do zwrotu osi x. Pod jaką siłą się to dzieje? Jakie jest przyspieszenie układu/

zi: 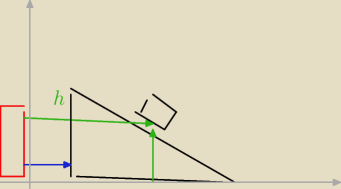Zadanie jest b.łatwe do rozwiązania jeśli używasz metody zapisu "x i dwie kropki ponad jako zapis pochodnej po czasie", wtedy tylko potrzeba szukać tego co tylko ty wiesz o zadaniu (a nie Izaak Newton) czyli równanie "więzów" tzn. przedmioty reagują tylko na to co "dał im Newton", natomiast resztę zna tylko filozof, czyli ten kto zrobi rysunek sytuacji. Newton nie zna tej sytuacji, tylko ty znasz. metoda polega na tym, że wybierasz sobie coś nieruchomego do opisu położeń x1 x2 y1 y2 np. może to być cegła postawiona gdzieś obok. Wtedy najważniejsze jest poszukanie takiego związku który jest stały dla danej sytuacji. tutaj stały jest kąt równi pochyłej do poziomu. Trzeba to zapisać przy pomocy położeń x1, x2, y1, y2 względem swojej cegły; wtedy to równanie które opisuje tzw. więzy czyli coś stałego w tej sytuacji to: { [ h − y1 ] / [ x1 −x2] } = tgα => h−y1=tgα [x1−x2] => druga pochodna po czasie z tego daje dużo pomocy. jedynka w indeksie oznacza ciało zsuwające się dalej już jest łatwo, lecz musisz używać zapisu pochodnych po czasie tzn, że druga pochodna położenia po czasie oznacza przyspieszenie (i w ten sposób zapisać to co daje Newton) 2) można to pewnie rozwiązać inną metodą używając zapisu z "siłami bezwładności" 3) rozwiązywanie tego zadania metodą szkolną, bez użycia układu odniesienia i położeń jest takie jak to opisałaś.

zi: mój wynik to przyspieszenie klocka oś x: (R/m)sinα oś y: (R/m)cosα − g przyspieszenie równi oś x: −(R/M)sinα (jest przeciwne do tego co ma klocek i odpowiednio mniejsze, M w mianowniku) oś y: jak myślisz? gdzie R to wartość siły reakcji pomiędzy klockiem a równią R= [g cosα] / [ (1/m) − (sin²α/M) ]

Anka: No tak, teraz to faktycznie wygląda banalnie, aż się dziwię, że nie zrobiłam tego... dziękuję.

daras: skoro to cie zabiło to powinnaś jeszcze trochę postudiować ale gdyby nie zabiło to by wzmocniło, podobno